1 Hallar el área del triángulo cuyos vértices son los puntos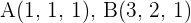 
y 
.
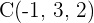Calculamos el producto vectorial
Obtenemos el módulo del vector resultante
Usamos la fórmula para obtener el área
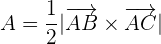
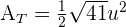
2 Hallar el volumen del tetraedro cuyos vértices son los puntos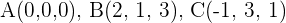 
y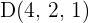 
.
Usamos la fórmula del volumen y obtenemos
3 Calcular la distancia entre las rectas: 
y 
encontramos el vector
Calculamos el producto mixto de los vectores
Calculamos el producto vectorial de los vectores directores y el modulo del vector resultante
Por tanto
4 Hallar el simétrico del punto A(3, 2, 1) respecto del plano 
En primer lugar calculamos 
, que es la recta que pasa por 
y es perpendicular a 
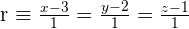
Hallamos el punto de intersección de la recta y el plano
Teniendo en cuenta las coordenadas del punto medio de un segmento, podemos hallar el extremo 
, resolviendo
obtenemos
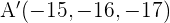
5 Calcular el área del triángulo cuyos vértices son los puntos de intersección del plano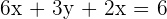 
con los ejes coordenados.
Ahora bien, el triángulo está formado por lo vectores
Calculamos el producto vectorial
Por tanto el area es
6 Dado el plano de ecuación 
y el punto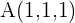 
hallar las coordenadas del pie de la perpendicular trazada desde a ese plano (o sea, la proyección ortogonal de sobre él).
Buscamos la recta perpendicular a que pasa por . El vector normal del plano es paralelo a esta recta, por lo tanto lo tomaremos como vector director:
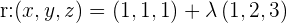
Ahora buscamos la intersección de la recta con el plano, reemplazando las ecuaciones paramétricas de la recta en la ecuación del plano:
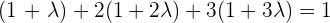
Reemplazamos en la ecuación de la recta para obtener as coordenadas del punto y obtenemos
7 Determinar la ecuación del plano que está a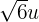 
de distancia del origen y es paralelo a aquel que tiene por ecuación 
.
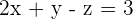Puesto que es paralelo al plano 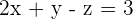, este tendra la siguiente forma
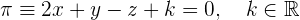
Además, dista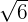 
unidades del origen, entonces
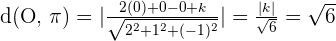
De lo anterior tenemos que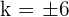 
, por lo tanto tendremos dos posibles planos
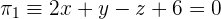
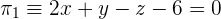
8 Hallar la distancia entre el punto 
y la recta del primer octante.
Tenemos que el primer octante es el recinto comprendido por los ejes, en su parte positiva, por tanto la recta diagonal de este octante pasa por el origen, es decir el punto 
y tiene como vector director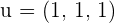 
.
Aplicando
con 
. Entonces
Calculamos la magnitud de 
y 
Por lo tanto
9 Calcular la distancia entre los planos:
de 
entre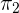 
, y este debe ser igual al cociente de los coeficientes de y, y de z. Sin embargo debe ser diferente el cociente de los términos independientes, pues si no, los planos no serían paralelos, sino iguales. 
Los dos planos son paralelos.
Transformamos la ecuación del segundo plano para que los dos planos tengan el mismo vector normal.
Usamos la fórmula de la distancia entre dos planos paralelos
¿Buscas profesor de matemáticas? Superprof es tu sitio.
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
No me queda claro por qué el área de un paralelogramo con los vectores ā y ē es |ā x ē| en vez de ser |ā|·|ē| que sería el módulo (longitud) de uno por el módulo (longitud) del otro.
Para entenderlo recordemos cómo se calcula el área del paralelogramo es base por altura, para la base se toma el módulo de uno de los vectores pero para altura se toma la proyección del otro vector en el eje vertical lo que implica la función seno y ya multiplicados dan una de las definiciones del producto cruz, en el artículo “https://www.superprof.es/apuntes/escolar/matematicas/analitica/distancias/areas-y-volumenes.html#tema_area-del-paralelogramo” se la imagen de lo que explique.