
Definiciones importantes sobre vectores
Vectores equipolentes
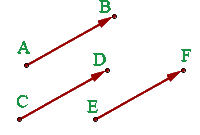
Dos vectores son equipolentes cuando tienen igual módulo, dirección y sentido.
Vectores libres

El conjunto de todos los vectores equipolentes entre sí se llama vector libre. Es decir los vectores libres tienen el mismo módulo, dirección y sentido.
Vectores fijos
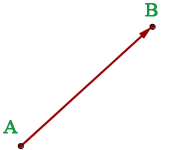
Un vector fijo es un representante del vector libre. Es decir, los vectores fijos tienen el mismo módulo, dirección, sentido y origen.
Vectores ligados

Los vectores ligados son vectores equipolentes que actúan en la misma recta. Es decir, los vectores fijos tienen el mismo módulo, dirección, sentido y se encuentran en la misma recta.
Vectores opuestos

Los vectores opuestos tienen el mismo módulo, dirección, y distinto sentido.
Vectores unitarios

Los vectores untario tienen de módulo, la unidad. Esto quiere decir que un vector  es unitario si
es unitario si

Para obtener un vector unitario, de la misma dirección y sentido que el vector dado se divide éste por su módulo.
Vectores concurrentes

Los vectores concurrentes tienen el mismo origen.
Vector de posición
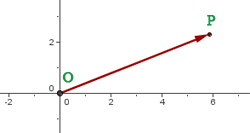
El vector  que une el origen de coordenadas
que une el origen de coordenadas  con un punto
con un punto  se llama vector de posición del punto
se llama vector de posición del punto  .
.
Vectores linealmente independientes
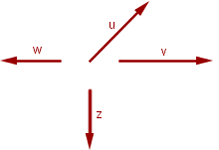
Hay dos formas principales de definir esto. La primera es que varios vectores libres del plano son linealmente independientes si ninguno puede expresarse como una combinación lineal de los demás. La segunda es que varios vectores libres del plano son linealmente independientes si es que si existe una combinación lineal de ellos que sea igual al vector cero, sin que sean cero todos los coeficientes de la combinación lineal. Esto es, los vectores 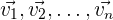 son linealmente independientes si existen números reales
son linealmente independientes si existen números reales  no todos cero (al menos algún
no todos cero (al menos algún  ) tal que
) tal que
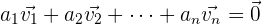
Vectores linealmente dependientes

De igual manera hay dos formas principales de definir esto. La primera es que varios vectores libres del plano son linealmente dependientes si alguno puede expresarse como una combinación lineal de los demás. La segunda es que varios vectores libres del plano son linealmente dependientes si la única manera de que una combinación lineal de estos sea igual al vector cero es que todos los coeficientes sean igual al escalar cero. Esto es, tenemos que si se cumple que
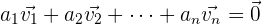
entonces esto solo puede pasar si
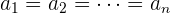
Vectores ortogonales
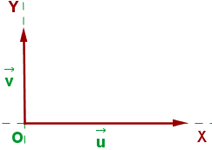
Dos vectores son ortogonales o perpendiculares si su producto escalar es cero. Esto es, los vectores  y
y  son ortogonales si y sólo si
son ortogonales si y sólo si
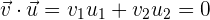 .
.
Vectores ortonormales
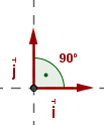
Dos vectores  y
y  son ortonormales si cumplen los siguiente:
son ortonormales si cumplen los siguiente:
-
- Son ortogonales:
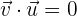
- Son ortogonales:
- Son unitarios:

Ejemplos sobre vectores
1. Dado el vector 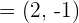 , determinar dos vectores equipolentes a
, determinar dos vectores equipolentes a  ,
,  y
y 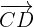 , sabiendo que
, sabiendo que 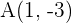 y
y 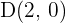 .
.
Para resolver este ejercicio, notemos que  es el vector posición del punto
es el vector posición del punto  , y notemos que
, y notemos que 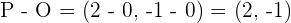 (
( es el origen), esto es, el vector está definido por la diferencia de los puntos que une, así, todo vector equipolente a
es el origen), esto es, el vector está definido por la diferencia de los puntos que une, así, todo vector equipolente a  debe cumplir que el punto final menos el inicial es igual a
debe cumplir que el punto final menos el inicial es igual a 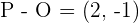 . Dicho esto, tenemos el punto inicial del vector
. Dicho esto, tenemos el punto inicial del vector  ,
, 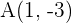 , ahora solo debemos encontrar el punto final
, ahora solo debemos encontrar el punto final  , eso lo haremos de la siguiente manera
, eso lo haremos de la siguiente manera

Esto nos dice que  . Ahora encontraremos el punto inicial del vector
. Ahora encontraremos el punto inicial del vector 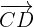 , dado que ya conocemos el final
, dado que ya conocemos el final 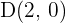
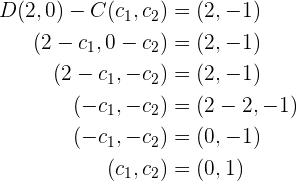
Esto nos dice que  .
.
2. Calcula las coordenadas de  para que el cuadrilátero de vértices:
para que el cuadrilátero de vértices: 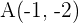 ,
, 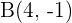 ,
, 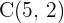 y
y  ; sea un paralelogramo.
; sea un paralelogramo.
Nuestro paralelogramo se muestra en la siguiente imagen

Nuestra tarea es encontrar las coordenadas de  . Para esto procederemos igual que en el ejercicio anterior. Tenemos que los vectores
. Para esto procederemos igual que en el ejercicio anterior. Tenemos que los vectores  y
y 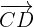 deben de ser vectores equipolentes, por lo tanto, tenemos que
deben de ser vectores equipolentes, por lo tanto, tenemos que 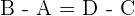 . Por medio de esta igualdad despejaremos los valores de las coordenadas del punto
. Por medio de esta igualdad despejaremos los valores de las coordenadas del punto 
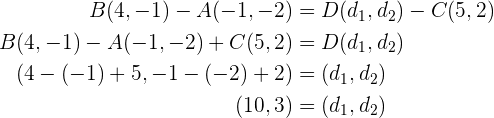
Así, nuestro punto es 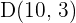 .
.
3. Si  es un vector de componentes
es un vector de componentes  , hallar un vector unitario de su misma dirección y sentido.
, hallar un vector unitario de su misma dirección y sentido.
Para resolver esto primero obtendremos la magnitud de nuestro vector
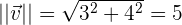
Nuestro vector deseado es simplemente el vector  entre su magnitud, esto es
entre su magnitud, esto es

4. Hallar un vector unitario de la misma dirección que el vector 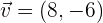 .
.
Para resolver esto primero obtendremos la magnitud de nuestro vector
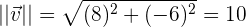
Nuestro vector deseado es simplemente el vector  entre su magnitud, esto es
entre su magnitud, esto es
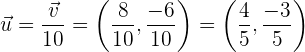 .
.
Notemos que el vector 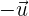 también es unitario, tiene la misma dirección, pero tiene sentido opuesto.
también es unitario, tiene la misma dirección, pero tiene sentido opuesto.
5. Hallar un vector unitario  que tenga la misma dirección que el vector
que tenga la misma dirección que el vector 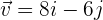
Para resolver esto primero obtendremos la magnitud de nuestro vector
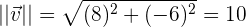
Nuestro vector deseado es simplemente el vector  entre su magnitud, esto es
entre su magnitud, esto es
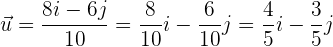 .
.
Notemos que el vector 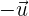 también es unitario, tiene la misma dirección, pero tiene sentido opuesto.
también es unitario, tiene la misma dirección, pero tiene sentido opuesto.
Encuentra a tu profesor de matemáticas ideal en Madrid gracias a Superprof.













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Sean u = 2i − 3j y v = −4i + 6j. Encuentre: 4v − 6u , con su bosquejo
Al trasladar el punto A(2,4) dado el vector B(2-2) se obtiene?
Hola, de la matriz que calcularon la determinante no es =0.
Podrías señalar el ejercicio para rectificar por favor.
Calcular x²+1
Cómo resolver los ejercicios si están en kilómetros por ejemplo:
A= 300km b=4,000km C= 5,000km
Osea cuando sustituimos tenemos que poner √(X1,X2)² + (Y1,X2)²
O (X2,X1)² +(Y2,Y1)²
¿Cual de las dos?
Depende de que quieras obtener y que significa la expresión (X1,X2), la expresión √(X1,X2)² + (Y1,X2)² esta mal escrita si quieres encontrar una distancia.
24 4 70 NE
Vectores modelo