Temas

Base
Dos vectores en el plano  y
y  son linealmente independiente, si
son linealmente independiente, si 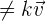 para toda constante
para toda constante  . Dichos vectores linealmente independientes, con distintas direcciones, forman una base, porque cualquier vector del plano puede ser escrito como combinación lineal de
. Dichos vectores linealmente independientes, con distintas direcciones, forman una base, porque cualquier vector del plano puede ser escrito como combinación lineal de  y
y  , esto es, dado un vector
, esto es, dado un vector 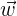 ,
,
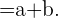
Como primer ejemplo tenemos la siguiente grafica,
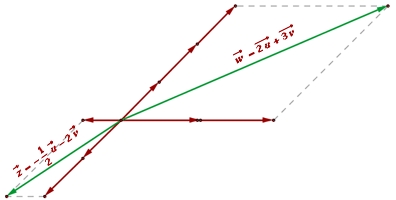
Las coordenadas del vector 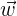 respecto a la base definida por
respecto a la base definida por  y
y  estan dadas por
estan dadas por
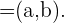
Ejemplos
1 Dados lo siguiente vectores obtener sus coordenadas respecto a la base definida por  y
y  .
.
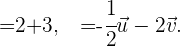
Como solución tenemos que las coordenadas estan dadas por
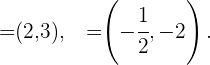
2 Que pares de los siguiente vectores forman una base,
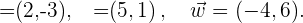
Para saber si dos vectores  y
y 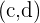 forman una base, comprobamos si la siguiente igualdad no se satisfaga,
forman una base, comprobamos si la siguiente igualdad no se satisfaga,

Para la pareja  , tenemos
, tenemos
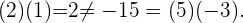
Por lo tanto  forman una base.
forman una base.
Para la pareja  , tenemos
, tenemos
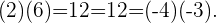
Por lo tanto  no forman una base.
no forman una base.
Para la pareja  , tenemos
, tenemos
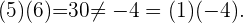
Por lo tanto  forman una base.
forman una base.
Sistemas de referencia
En el plano un sistema de referencia esta formado por un punto  y un plano
y un plano 
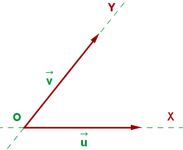
EL punto  del sistema de referencia se llama origen y los vectores linealmente independientes
del sistema de referencia se llama origen y los vectores linealmente independientes 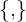 forman una base.
forman una base.
Sistema de referencia ortogonal
Un sistema de referencia se dice ortogonal si los vectores  son una base perpendicular y tienen distinto modulo,
son una base perpendicular y tienen distinto modulo,
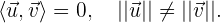

Sistema de referencia ortonormal
Un sistema de referencia se dice ortonormal si los vectores  son una base perpendicular y tienen modulo unitario,
son una base perpendicular y tienen modulo unitario,
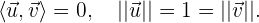

EL ejemplo más importante de una base ortonormal es la base canónica, esta compuesta por los siguiente vectores,

Recordemos que las rectas  y
y  se llaman ejes coordenados o ejes coordenados cartesianos. En los siguiente veremos algunos ejemplos,
se llaman ejes coordenados o ejes coordenados cartesianos. En los siguiente veremos algunos ejemplos,
Ejemplos.
1 Dados los vectores 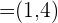 y
y 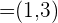 que constituyen una base. Expresar en esta base al vector
que constituyen una base. Expresar en esta base al vector 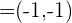 .
.
Consideramos la siguiente ecuación
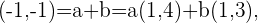
luego obtenemos las siguientes ecuaciones
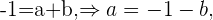

Finalmente  Lo que nos da que
Lo que nos da que 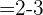 .
.
2 Dados los vectores 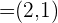 ,
, 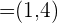 y
y 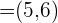 . Determinar:
. Determinar:
A Si los vectores  y
y  forman una base.
forman una base.
Para comprobar esto, vemos si el producto de la primera coordenada de  con la segunda coordenada de
con la segunda coordenada de  es diferente al producto de la primera coordenada de
es diferente al producto de la primera coordenada de  con la segunda coordenada de
con la segunda coordenada de  ,
,

Por lo tanto podemos concluir que si forman una base.
B Expresar a 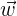 como una combinación de los elementos de la base formada por
como una combinación de los elementos de la base formada por  y
y  .
.
Consideramos la siguiente ecuación
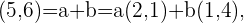
luego obtenemos las siguientes ecuaciones
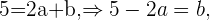

Finalmente 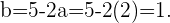 Lo que nos da que
Lo que nos da que 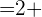 .
.
C Dado el vector 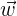 con coordenadas
con coordenadas  en la base canonica. Que coordenadas tendrá en la base formanada por
en la base canonica. Que coordenadas tendrá en la base formanada por  y
y  .
.
De nuevo formamos el siguiente sistema de ecuaciones,
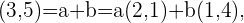
luego obtenemos las siguientes ecuaciones
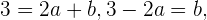

Finalmente 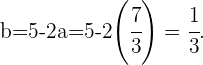 Lo que nos da que las coordenadas ene la base de
Lo que nos da que las coordenadas ene la base de  y
y  son
son 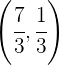 .
.
D Dados los vectores 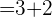 ,
, 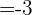 y
y 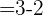 . Calcular las coordenadas de
. Calcular las coordenadas de 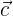 en la base
en la base  y
y  .
.
Ahora reemplazamos las expresiones para  y
y  en
en 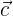 ,
,
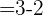



Por lo tanto las coordenadas para 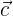 son
son 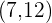 .
.
Encuentra a tu profesor matematicas en Superprof.













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Sean u = 2i − 3j y v = −4i + 6j. Encuentre: 4v − 6u , con su bosquejo
Al trasladar el punto A(2,4) dado el vector B(2-2) se obtiene?
Hola, de la matriz que calcularon la determinante no es =0.
Podrías señalar el ejercicio para rectificar por favor.
Calcular x²+1
Cómo resolver los ejercicios si están en kilómetros por ejemplo:
A= 300km b=4,000km C= 5,000km
Osea cuando sustituimos tenemos que poner √(X1,X2)² + (Y1,X2)²
O (X2,X1)² +(Y2,Y1)²
¿Cual de las dos?
Depende de que quieras obtener y que significa la expresión (X1,X2), la expresión √(X1,X2)² + (Y1,X2)² esta mal escrita si quieres encontrar una distancia.
24 4 70 NE
Vectores modelo