Temas

Definición de las componentes de un vector
Consideremos los puntos 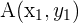 y
y 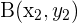 y el vector
y el vector  que va del punto
que va del punto  al punto
al punto  como se muestra en la siguiente figura:
como se muestra en la siguiente figura:
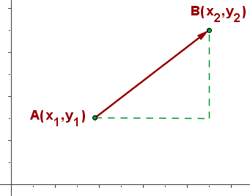
Definimos las componentes del vector  como las coordenadas del punto extremo
como las coordenadas del punto extremo  menos las coordenadas del punto origen
menos las coordenadas del punto origen  , es decir,
, es decir,

Algunas veces, los vectores se suelen escribir de la forma

donde  es la primera componente y
es la primera componente y  es la segunda componente. Por lo tanto,
es la segunda componente. Por lo tanto,

A  y
y  se les conoce como vectores canónicos. Esta es sólo otra manera de escribir un vector.
se les conoce como vectores canónicos. Esta es sólo otra manera de escribir un vector.
En general, los componentes de un vector también de pueden llamar coordenadas. Sin embargo, esto no es lo más apropiado en este contexto. El motivo es que las coordenadas son números que nos permiten encontrar algún objeto en el plano o espacio, y los componentes del vector no nos ayudan a localizarlo en el plano.
Aplicación en colinealidad de puntos
Consideremos tres puntos 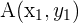 ,
, 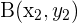 y
y 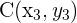 . Entonces podemos utilizar vectores para determinar si estos puntos son colineales (es decir, se encuentran los tres sobre una misma línea). También se dice que los puntos
. Entonces podemos utilizar vectores para determinar si estos puntos son colineales (es decir, se encuentran los tres sobre una misma línea). También se dice que los puntos  ,
,  y
y  están alineados.
están alineados.
Recordemos que dos vectores son paralelos si uno es el múltiplo escalar de otro. Es decir 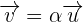 . Por lo tanto,
. Por lo tanto,  ,
,  y
y  serán colineales si
serán colineales si
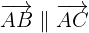
Es decir,

que sustituyendo sus componentes, tenemos

Es decir,

Luego, si despejamos  en ambas ecuaciones, tenemos,
en ambas ecuaciones, tenemos,
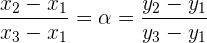
Por lo tanto, tres puntos serán colineales si se satisface

Ejercicios propuestos
1 Calcula los componentes del vector  , cuyos extremos son los puntos
, cuyos extremos son los puntos

Simplemente aplicamos la fórmula que se nos dió al principio:
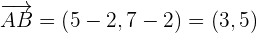
2 Un vector  tiene componentes
tiene componentes  . Encuentra las coordenadas de
. Encuentra las coordenadas de  si se sabe que
si se sabe que 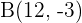 .
.
En este caso consideramos unos componentes arbitrarios para  , es decir,
, es decir, 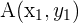 . Entonces, al utilizar la fórmula obtenemos
. Entonces, al utilizar la fórmula obtenemos

Por lo tanto, los componentes deben ser igual, es decir,

Al despejar  y
y  , obtenemos
, obtenemos

Por lo tanto,  .
.
3 Considera los puntos  ,
, 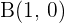 y
y 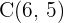 . ¿Se encuentran alineados?
. ¿Se encuentran alineados?
Para saber si los puntos están alineados, simplemente verificamos que se cumpla la relación que probamos anteriormente. Primero revisamos la proporción en los componentes  :
:
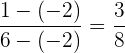
y después revisamos la proporción en los componentes  :
:
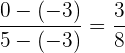
Por lo tanto, como las dos proporciones son iguales, concluímos que los puntos sí están alineados.
4 Considera los puntos  ,
, 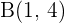 y
y 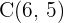 . ¿Se encuentran alineados?
. ¿Se encuentran alineados?
De forma similar al ejercicio anterior, para saber si los puntos están alineados, verificaremos que se cumpla la relación que probamos anteriormente. Primero revisamos la proporción en los componentes  :
:
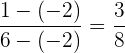
Luego, revisamos la proporción en los componentes  :
:
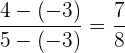
En este caso las proporciones no son iguales, por lo tanto, puntos no son colineales.
5 Encuentra el valor de  para que los puntos
para que los puntos  ,
,  y
y 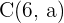 estén alineados.
estén alineados.
Si los puntos están alineados, entonces tenemos que se cumple

El lado izquierdo de esta igualdad nos da
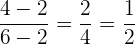
Por lo tanto, al multiplicar por 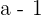 la igualdad, obtenemos
la igualdad, obtenemos

Es decir,  .
.
6 Dados los puntos  y
y 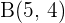 , encuentra un punto
, encuentra un punto  que esté alineado a
que esté alineado a  y
y  . Además, el vector
. Además, el vector 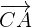 debe ser
debe ser  veces más largo que
veces más largo que 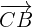 , es decir,
, es decir,

Notemos que, por el hecho de tener que

entonces los puntos serán colineales. Denotemos al punto  como
como 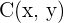 , entonces
, entonces

Así, se debe cumplir
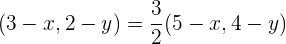
de aquí se obtienen las siguientes ecuaciones:
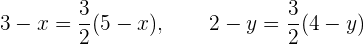
Al resolverlas, obtenemos 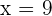 y
y 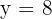 . Por lo tanto, el punto
. Por lo tanto, el punto  es
es
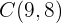
Ejercicios de punto medio de dos puntos y baricentros
Recordemos que dados dos puntos 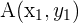 y
y 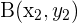 , el punto medio de estos dos puntos se calcula mediante:
, el punto medio de estos dos puntos se calcula mediante:

En la siguiente figura se puede apreciar el punto medio de  y
y  :
:

Además, se dice que el punto  es simétrico de
es simétrico de  respecto a
respecto a  si
si  es el punto medio del segmento
es el punto medio del segmento  .
.
En general, si queremos encontrar un punto  que divida el segmento de recta de forma que cumpla una razón
que divida el segmento de recta de forma que cumpla una razón

entonces utilizamos
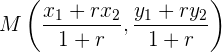
Similarmente, dado un triángulo con vértices 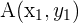 ,
, 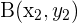 y
y 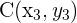 , entonces las coordenadas del baricentro son
, entonces las coordenadas del baricentro son
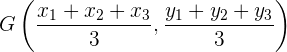
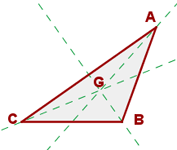
El baricentro de un triángulo se observa en la siguiente figura:
7 Calcula las coordenadas del punto medio del segmento  , donde
, donde 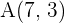 y
y 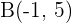 .
.
Para este caso, sólo utilizamos la fórmula del punto medio:
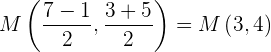
8 Calcula:
a el punto simétrico de 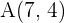 respecto al punto
respecto al punto 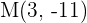 ,
,
b el punto simétrico a 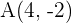 respecto de
respecto de 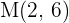 .
.
a Denotemos al punto simétrico de  como
como  . Entonces
. Entonces  es el punto medio del segmento
es el punto medio del segmento  . Por tanto, si
. Por tanto, si  tiene coordenadas
tiene coordenadas 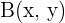 , entonces
, entonces  se calcula utilizando
se calcula utilizando
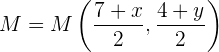
Pero, además, se tiene que 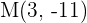 . Por lo tanto,
. Por lo tanto,
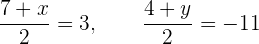
Si multiplicamos por 2 ambas ecuaciones, obtenemos

Por lo tanto, al despejar tenemos  y
y 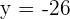 . Es decir, el punto simétrico es
. Es decir, el punto simétrico es 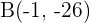 .
.
b De forma similar, denotaremos al punto simétrico como 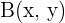 . Así,
. Así,  se calcula utilizando
se calcula utilizando
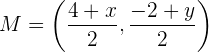
Pero, además, se tiene que 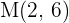 . Por lo tanto,
. Por lo tanto,
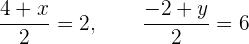
Si multiplicamos por 2 ambas ecuaciones, obtenemos

Por lo tanto, al despejar tenemos  y
y 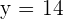 . Es decir, el punto simétrico es
. Es decir, el punto simétrico es 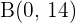 .
.
9 Encuentra las coordenadas del baricentro para:
a un triángulo con vértices en 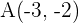 ,
, 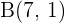 y
y  ,
,
b el triángulo con vértices  ,
,  y
y  .
.
En este ejercicio sólo debemos utilizar la fórmula del baricéntro de un triángulo. Así:
a Para el primer inciso tenemos
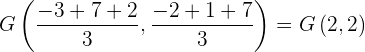
b Mientras que para el segundo inciso tenemos

10 Calcula los puntos  y
y  que dividen al segmento
que dividen al segmento  , cuyos extremos son
, cuyos extremos son  y
y 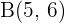 , en tres partes iguales.
, en tres partes iguales.
Notemos que debemos encontrar dos puntos  y
y  tales que
tales que
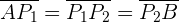
1 Para encontrar el primer punto, notemos que la razón es
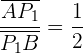
ya que el segmento del denominador mide el doble. Así, utilizamos la fórmula:

2 Similarmente, para encontrar el segundo punto ahora la razón es
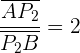
ya que, en este caso, el segmento del numerador mide el doble. Así, utilizamos la fórmula:

Por lo tanto, los puntos son  y
y 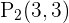 .
.
11 Encuentra las coordenadas del punto  , sabiendo que
, sabiendo que 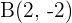 es el punto medio de
es el punto medio de  y que
y que 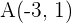 .
.
Denotemos las coordenadas del punto  como
como 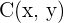 . Entonces,
. Entonces,  se calcula utilizando
se calcula utilizando
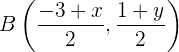
Además, tenemos que 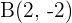 . Por tanto, tenemos las ecuaciones
. Por tanto, tenemos las ecuaciones

Si multiplicamos por 2 las ecuaciones, tenemos

Por lo tanto, al despejarlas, obtenemos que  y
y 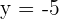 . Así, el punto es
. Así, el punto es
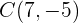
12 Considera el segmento  con extremos
con extremos 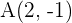 y
y  . Encuentra las coordenadas del punto
. Encuentra las coordenadas del punto  que divide al semento
que divide al semento  en dos segmentos tales que
en dos segmentos tales que  es la mitad de
es la mitad de  .
.
Como  es la mitad de
es la mitad de  , entonces tenemos
, entonces tenemos
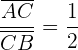
Por tanto, sólo utilizamos la fórmula:

Así, el punto es 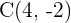 .
.
13 Si el segmento  con extremos
con extremos 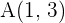 y
y 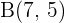 se divide en cuatro partes iguales, ¿cuáles son las coordenadas de los puntos de división?
se divide en cuatro partes iguales, ¿cuáles son las coordenadas de los puntos de división?
Buscaremos 3 puntos  ,
,  y
y  tales que
tales que
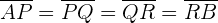
tal y como se muestra en la siguiente figura:

1 Para calcular  , notemos que
, notemos que
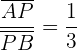
ya que el segmento de  a
a  medirá la tercera parte del segmento que va de
medirá la tercera parte del segmento que va de  a
a  . Así, utilizamos la fórmula para calcular
. Así, utilizamos la fórmula para calcular  :
:

2 Observemos que  es el punto medio entre
es el punto medio entre  y
y  , por lo que se calcula utilizando
, por lo que se calcula utilizando

3 Por último, para  tenemos
tenemos

ya que el segmento de  a
a  medirá tres veces la longitud del segmento que va de
medirá tres veces la longitud del segmento que va de  a
a  . Así, utilizamos la fórmula para calcular
. Así, utilizamos la fórmula para calcular  :
:

Por lo tanto, lo puntos son
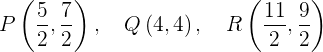
14 Considera un triángulo donde dos de sus vértices son  y
y 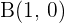 . Si el baricentro del triángulo es
. Si el baricentro del triángulo es  , ¿cuáles son las coordenadas del tercer vértice
, ¿cuáles son las coordenadas del tercer vértice  ?
?
Denotemos las coordenadas de  como
como 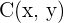 . Entonces el baricentro se calcula utilizando
. Entonces el baricentro se calcula utilizando

Pero también tenemos que  , por lo que
, por lo que
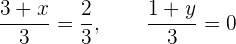
Multiplicando por 3, obtenemos

De aquí se sigue que  y
y  . Por lo tanto, el vértice
. Por lo tanto, el vértice  es
es

15 Dados los puntos  y
y 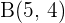 , encuentra un punto
, encuentra un punto  que esté alineado con
que esté alineado con  y
y  , y que cumpla con la relación
, y que cumpla con la relación

La fórmula que tenemos para puntos medios o puntos que parten un segmento en una razón dada siempre se utiliza con puntos colineales. Por lo tanto, utilizaremos esa fórmula.
Asimismo, veamos que ya se nos proporcionó la razón  , por lo que procedemos a utilizar la fórmula:
, por lo que procedemos a utilizar la fórmula:

Es decir, el punto  es
es
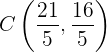













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Sean u = 2i − 3j y v = −4i + 6j. Encuentre: 4v − 6u , con su bosquejo
Al trasladar el punto A(2,4) dado el vector B(2-2) se obtiene?
Hola, de la matriz que calcularon la determinante no es =0.
Podrías señalar el ejercicio para rectificar por favor.
Calcular x²+1
Cómo resolver los ejercicios si están en kilómetros por ejemplo:
A= 300km b=4,000km C= 5,000km
Osea cuando sustituimos tenemos que poner √(X1,X2)² + (Y1,X2)²
O (X2,X1)² +(Y2,Y1)²
¿Cual de las dos?
Depende de que quieras obtener y que significa la expresión (X1,X2), la expresión √(X1,X2)² + (Y1,X2)² esta mal escrita si quieres encontrar una distancia.
24 4 70 NE
Vectores modelo