
Fórmula del ángulo entre dos vectores
El ángulo que forman dos vectores  y
y  viene dado por la expresión:
viene dado por la expresión:
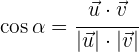
La expresión en función de sus coordenadas es

Ejemplo: Hallar el ángulo comprendido entre los vectores  y
y 
1Para emplear la fórmula que permite encontrar el ángulo comprendido entre dos vectores, primero calculamos el producto de los dos vectores
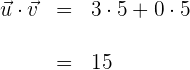
2Calculamos la magnitud del primer vector
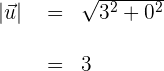
3Calculamos la magnitud del segundo vector

4Sustituimos los valores previamente obtenidos, en la fórmula del ángulo  entre dos vectores
entre dos vectores
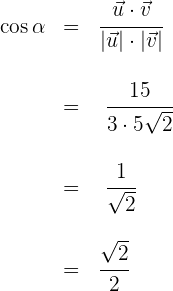
5El valor  que satisface la igualdad anterior es
que satisface la igualdad anterior es 
Ejercicios propuestos
1Calcular el producto escalar y el ángulo que forman los vectores  .
.
1Para emplear la fórmula que permite encontrar el ángulo comprendido entre dos vectores, primero calculamos el producto de los dos vectores

2Calculamos la magnitud del primer vector

3Calculamos la magnitud del segundo vector

4Sustituimos los valores previamente obtenidos, en la fórmula del ángulo  entre dos vectores
entre dos vectores

5El valor  que satisface la igualdad anterior es
que satisface la igualdad anterior es 
¿Y si pruebas nuestras clases particulares de matematicas?
2Calcular el producto escalar y el ángulo que forman los vectores  .
.
1Para emplear la fórmula que permite encontrar el ángulo comprendido entre dos vectores, primero calculamos el producto de los dos vectores

2Calculamos la magnitud del primer vector
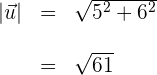
3Calculamos la magnitud del segundo vector

4Sustituimos los valores previamente obtenidos, en la fórmula del ángulo  entre dos vectores
entre dos vectores

5El valor  que satisface la igualdad anterior es
que satisface la igualdad anterior es 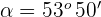
3Calcular el producto escalar y el ángulo que forman los vectores  .
.
1Para emplear la fórmula que permite encontrar el ángulo comprendido entre dos vectores, primero calculamos el producto de los dos vectores
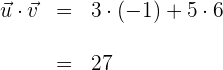
2Calculamos la magnitud del primer vector

3Calculamos la magnitud del segundo vector
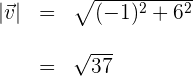
4Sustituimos los valores previamente obtenidos, en la fórmula del ángulo  entre dos vectores
entre dos vectores

5El valor  que satisface la igualdad anterior es
que satisface la igualdad anterior es 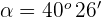
4Dados los vectores 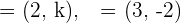 , calcula
, calcula  para que los vectores
para que los vectores  y
y  sean perpendiculares.
sean perpendiculares.
1A partir de la fórmula del ángulo entre dos vectores, se obtiene
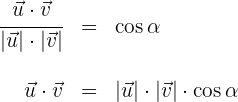
2Calculamos el producto interno de los vectores
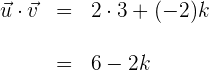
3Dos vectores son perpendiculares si el ángulo entre ellos es de  ; el coseno de este ángulo es cero
; el coseno de este ángulo es cero
4Calculamos la magnitud del primer vector
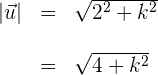
5Calculamos la magnitud del segundo vector

6Sustituimos en la fórmula inicial los valores previamente obtenidos y resolvemos para 

Así, el valor buscado es 
5Dados los vectores 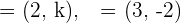 , calcula
, calcula  para que los vectores
para que los vectores  y
y  sean paralelos.
sean paralelos.
1A partir de la fórmula del ángulo entre dos vectores, se obtiene
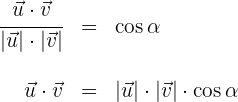
2Calculamos el producto interno de los vectores
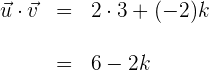
3Dos vectores son paralelos si el ángulo entre ellos es de 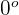 ; el coseno de este ángulo es uno
; el coseno de este ángulo es uno
4Calculamos la magnitud del primer vector
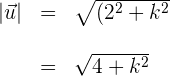
5Calculamos la magnitud del segundo vector

6Sustituimos en la fórmula inicial los valores previamente obtenidos y resolvemos para 

Así, el valor buscado es 
Otra forma de resolver el ejercicio es considerar la proporcionalidad de sus componentes

6Dados los vectores 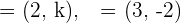 , calcula
, calcula  para que los vectores
para que los vectores  y
y  formen un ángulo de
formen un ángulo de  .
.
1A partir de la fórmula del ángulo entre dos vectores, se obtiene
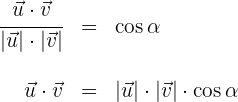
2Calculamos el producto interno de los vectores
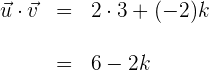
3El ángulo entre lo dos vectores es de  ; el coseno de este ángulo es
; el coseno de este ángulo es

4Calculamos la magnitud del primer vector
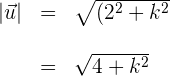
5Calculamos la magnitud del segundo vector

6Sustituimos en la fórmula inicial los valores previamente obtenidos y resolvemos para 

7Resolvemos empleando la fórmula para encontrar las raíces de la ecuación de segundo grado

Las raíces son  , pero solamente
, pero solamente 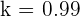 es solución de
es solución de  , ya que tuvimos que elevar al cuadrado para obtener las soluciones. Así, el valor buscado es
, ya que tuvimos que elevar al cuadrado para obtener las soluciones. Así, el valor buscado es 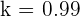 .
.
7Hallar  si el ángulo que forman
si el ángulo que forman  y
y 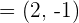 vale
vale  .
.
1A partir de la fórmula del ángulo entre dos vectores, se obtiene
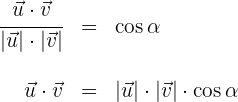
2Calculamos el producto interno de los vectores
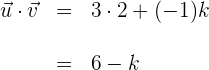
3El coseno de  es cero
es cero
4Calculamos la magnitud del primer vector

5Calculamos la magnitud del segundo vector

6Sustituimos en la fórmula inicial los valores previamente obtenidos y resolvemos para 

Así, el valor buscado es 
8Hallar  si el ángulo que forman
si el ángulo que forman  y
y 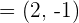 vale
vale 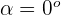 .
.
1A partir de la fórmula del ángulo entre dos vectores, se obtiene
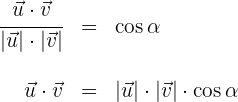
2Calculamos el producto interno de los vectores
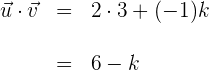
3El coseno de 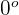 es uno
es uno
4Calculamos la magnitud del primer vector

5Calculamos la magnitud del segundo vector

6Sustituimos en la fórmula inicial los valores previamente obtenidos y resolvemos para 

Así, el valor buscado es 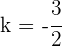
9Hallar  si el ángulo que forman
si el ángulo que forman  y
y 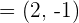 vale
vale  .
.
1A partir de la fórmula del ángulo entre dos vectores, se obtiene
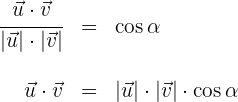
2Calculamos el producto interno de los vectores
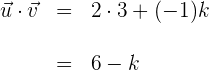
3El ángulo entre lo dos vectores es de  ; el coseno de este ángulo es
; el coseno de este ángulo es

4Calculamos la magnitud del primer vector
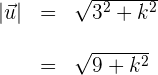
5Calculamos la magnitud del segundo vector

6Sustituimos en la fórmula inicial los valores previamente obtenidos y resolvemos para 

Las raíces son 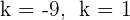
10Comprobar que el segmento de une los puntos medios de los lados  y
y  del triángulo:
del triángulo: 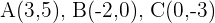 , es paralelo al lado
, es paralelo al lado  e igual a su mitad.
e igual a su mitad.
1Representamos gráficamente

2Calculamos el punto medio del lado 

3Calculamos el punto medio del lado 
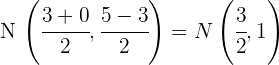
4Calculamos el vector 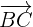
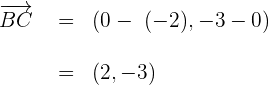
5Calculamos el vector 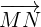
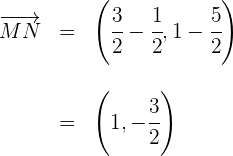
6Calculamos la magnitud del primer vector
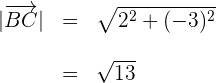
7Calculamos la magnitud del segundo vector
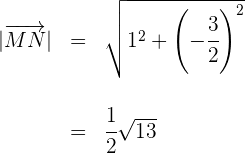
8Para verificar si los dos vectores son paralelos, verificamos la proporcionalidad de sus componentes

Como sus componentes son proporcionales, entonces los vectores son paralelos
11Calcular los ángulos del triángulo de vértices:  .
.
1Representamos gráficamente

2Calculamos el vector 
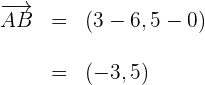
3Calculamos el vector 

4Calculamos la magnitud de 
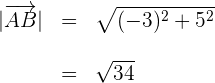
5Calculamos la magnitud de 

6Calculamos el producto interno de ambos vectores
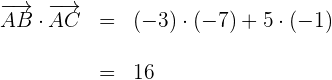
7Sustituimos los valores previamente obtenidos, en la fórmula del ángulo  entre dos vectores
entre dos vectores

El valor  corresondiente al vértice
corresondiente al vértice  que satisface la igualdad anterior es
que satisface la igualdad anterior es 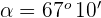
8Calculamos el vector 
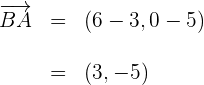
9Calculamos el vector 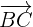
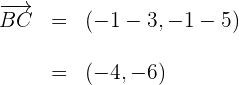
10Calculamos la magnitud de 

11Calculamos la magnitud de 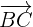

12Calculamos el producto interno de ambos vectores

13Sustituimos los valores previamente obtenidos, en la fórmula del ángulo  entre dos vectores
entre dos vectores

El valor  corresondiente al vértice
corresondiente al vértice  que satisface la igualdad anterior es
que satisface la igualdad anterior es 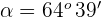
14Como la suma de os ángulos interiores de un triángulo es  , entonces el ángulo
, entonces el ángulo  correspondiente al vértice
correspondiente al vértice  es
es
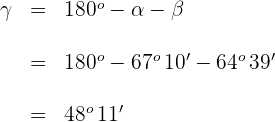













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Sean u = 2i − 3j y v = −4i + 6j. Encuentre: 4v − 6u , con su bosquejo
Al trasladar el punto A(2,4) dado el vector B(2-2) se obtiene?
Hola, de la matriz que calcularon la determinante no es =0.
Podrías señalar el ejercicio para rectificar por favor.
Calcular x²+1
Cómo resolver los ejercicios si están en kilómetros por ejemplo:
A= 300km b=4,000km C= 5,000km
Osea cuando sustituimos tenemos que poner √(X1,X2)² + (Y1,X2)²
O (X2,X1)² +(Y2,Y1)²
¿Cual de las dos?
Depende de que quieras obtener y que significa la expresión (X1,X2), la expresión √(X1,X2)² + (Y1,X2)² esta mal escrita si quieres encontrar una distancia.
24 4 70 NE
Vectores modelo