Temas
Las bisectrices de un triángulo son las rectas que dividen a cada ángulo del triángulo en dos ángulos iguales.

Incentro de un triángulo
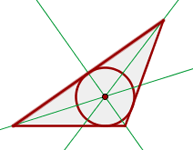
- El incentro es el punto de corte de las tres bisectrices.
- El incentro se expresa con la letra
 .
. - El incentro es el centro de una circunferencia inscrita en el triángulo.
Ejercicio para calcular las ecuaciones de las bisectrices e incentro
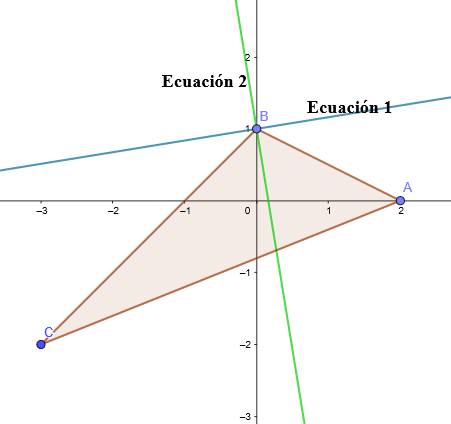
Hallar las ecuaciones de las bisectrices y el incentro del triángulo de vértices: y
y 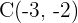 .
.

En primer lugar hallamos las ecuaciones de los lados del triángulo: para esto utilizaremos la forma punto-pendiente de la recta.
Recta formada por 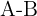 :
:
Calculamos la pendiente de la recta formada por los puntos  y
y 

utilizando esta pendiente y el punto  , obtenemos que la ecuación de la recta es
, obtenemos que la ecuación de la recta es

Recta formada por 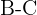 :
:
Pendiente de la recta formada por los puntos 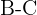

con la pendiente y el punto  obtenemos la recta
obtenemos la recta

Recta formada por 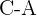 :
:
Tenemos que la pendiente de la recta formada por los puntos  y
y  es
es

con la pendiente y el punto  , tenemos que la ecuación de la recta es
, tenemos que la ecuación de la recta es

Cálculo de la bisectriz que pasa por A.
La teoría para el calculo de la ecuación de la bisectriz la puede encontrar aquí.
Para encontrar la ecuación de la bisectriz que pasa por  , consideramos las dos rectas que forman el ángulo
, consideramos las dos rectas que forman el ángulo
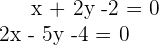
y 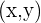 un punto sobre la bisectriz. Puesto que queremos que la distancia del punto a las rectas sea igual en ambos caso, debemos tener que
un punto sobre la bisectriz. Puesto que queremos que la distancia del punto a las rectas sea igual en ambos caso, debemos tener que

es decir, tendremos dos ecuaciones (una considerando el signo positivo y otra el signo negativo).
Primera ecuación:

entonces
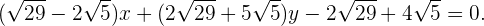
Si no se quiere trabajar con radicales se podría escribir una aproximación con números decimales, en este caso tendríamos

Segunda ecuación:

entonces
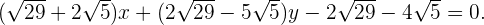
Con decimales seria aproximadamente
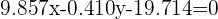
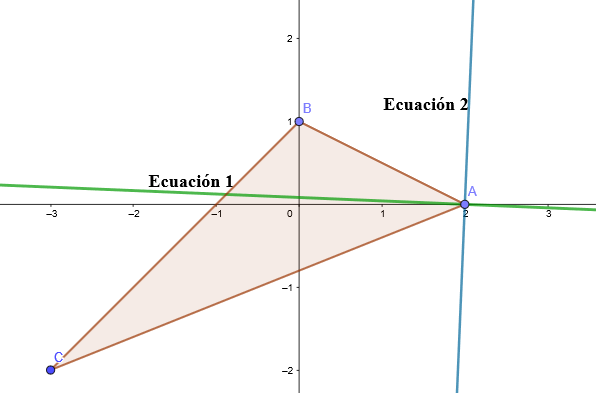
Cálculo de la bisectriz que pasa por B.
En este caso consideramos las ecuaciones de las dos rectas que pasan por 
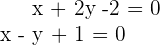
y 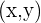 un punto sobre la bisectriz. En este caso debemos tener que
un punto sobre la bisectriz. En este caso debemos tener que

Primera ecuación:

Entonces

Con números decimales,
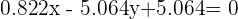
Segunda ecuación:
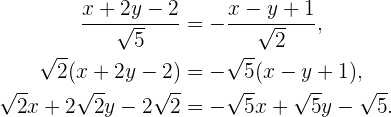
Entonces

con decimales sería aproximadamente

Cálculo de la bisectriz que pasa por C.
Para encontrar la ecuación de la bisectriz que pasa por  , consideramos las dos rectas que forman el ángulo
, consideramos las dos rectas que forman el ángulo
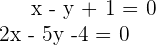
y 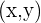 un punto sobre la bisectriz. Ahora bien
un punto sobre la bisectriz. Ahora bien

y las dos ecuaciones
Primera ecuación:

entonces
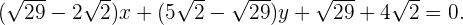
Con decimales
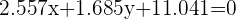
Segunda ecuación:

entonces
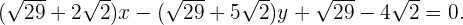
Escribiéndolo en su forma decimal
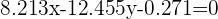
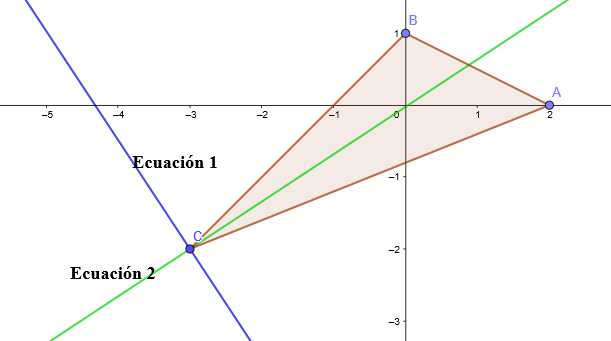
Calculo del incentro
El Incentro es el punto de corte de las tres bisectrices interiores. Para calcularlo, se resuelve el sistema formado por dos de las ecuaciones.
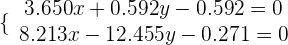
Resolviendo el sistema de ecuaciones con 2 incógnitas obtenemos que el incentro es


Área de la circunferencia inscrita
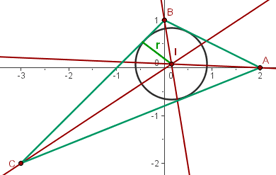
El incentro es el centro de la circunferencia inscrita en el triángulo, es decir, la circunferencia es tangente a los tres lados del triángulo. Por tanto, el radio de la circunferencia es la distancia del incentro a cualquiera de los lados.
Para calcular el área de la circunferencia debemos encontrar primero el radio, en este caso para encontrar el radio calcularemos la distancia de  al lado
al lado 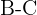 del triangulo
del triangulo

Por lo tanto tenemos que el área es
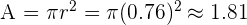













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
encuentre una forma general de una ecuación de la recta q pasa por el punto A q satisfaga la condicion dada A (5, – 2)
a) paralelo al eje y
b) perpendicular al eje y
¿Cuál es el lugar geométrico descrito por la trayectoria de un avión que se mantiene sobre volando la ciudad de San José a una distancia constante de 5 km de la Torre de Juan Santamaría
Graficar y calcular la distancia y punto Medio de los siguientes P(1,1),Q (3,3)
Hallar la distancia y la pendiente de A(07)
B(2,1)
F(×)=5-2×
A= (7,7)
B= (-9,-6)
Ecuación explícita de la recta
una recta pasa por el punto (0,-5) formando con una x un ángulo de x=90° Hallar la ecuación de la recta
1. Hallar las ecuaciones paramétricas de la recta que pasa por A(3,-1,0) y su vector director sea
perpendicular a los vectores: w = y u =