Capítulos
- Conociendo la base y la altura
- Conociendo dos lados y el ángulo que forman.
- Circunferencia circunscrita a un triángulo
- Circunferencia inscrita en un triángulo
- Fórmula de Herón
- Área de un triángulo conociendo las coordenadas de los vértices
- Área de un triángulo conociendo su vértices en el espacio
- Tres puntos alineados
Existen varias formas de encontrar el área de un triángulo, ello depende de los datos que se conozcan.
Conociendo la base y la altura
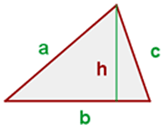
Si se conoce la base 
del triángulo y su altura 
, entonces la fórmula para encontrar el área viene dada por la mitad del producto de su base y su altura
Conociendo dos lados y el ángulo que forman.
Si se conocen dos lados del triángulo y el ángulo entre estos, entonces la fórmula para encontrar el área viene dada por la mitad del producto de los dos lados y el seno del ángulo entre estos
Circunferencia circunscrita a un triángulo
Si se conocen los tres lados 
del triángulo y el radio 
de la circunferencia circunscrita, entonces la fórmula para encontrar el área viene dada por el producto de los tres lados entre cuatro veces el radio de la circunferencia
Circunferencia inscrita en un triángulo
Si se conocen los tres lados del triángulo y el radio 
de la circunferencia inscrita, entonces la fórmula para encontrar el área viene dada por el producto del radio de la circunferencia por el semiperímetro del triángulo
El semiperímetro suele denotarse por
por lo que la fórmula del área suele expresarse por
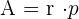
Fórmula de Herón
Si se conocen los tres lados del triángulo, entonces la fórmula para encontrar el área viene dada por
.
donde 
es el semiperímetro del triángulo
.
Área de un triángulo conociendo las coordenadas de los vértices
Cuando se conocen los vértices de un triángulo, se tienen dos formas de calcular el área
Área utilizando vectores
Conociendo los vértices 
del triángulo, el área es igual a la mitad del producto escalar, en valor absoluto, del vector perpendicular a 
por el vector 
.
Ejemplo: Calcular el área de un triángulo cuyos vértices son: 
y 
.
1Primero calculamos los vectores y
.
.
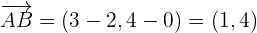2Calculamos el vector perpendicular a
.
3Aplicamos la fórmula para obtener el área del triángulo
.
Área por determinantes
Conociendo los vértices 
del triángulo, el área es igual a la mitad del valor absoluto del determinante de 
cuyas filas están conformadas por los vértices y en la tercera columna tienen el elemento uno
.
Para resolver el determinante de orden tres utilizamos la regla de Sarrus.
Ejemplo: Calcular el área de un triángulo cuyos vértices son: y .
1Primero sustituimos los vértices en la fórmula del área
.
2Aplicamos la regla de Sarrus para calcular el determinante
.
3Así, el área buscada es
.
Área de un triángulo conociendo su vértices en el espacio
Conociendo los vértices del triángulo, el área es igual a la mitad de la magnitud del producto vectorial de los vectores correspondientes a dos de sus lados
.
Ejemplo: Calcular el área de un triángulo cuyos vértices son: 
y 
.
1Primero calculamos los vectores de dos lados
.
.
2Calculamos el producto vectorial de 
y 
.
3Calculamos la magnitud de 
.
4Así, el área buscada es
.
Tres puntos alineados
Tres puntos están alineados cuando el área del triángulo es igual a cero.
Ejemplo: Averiguar si están alineados los puntos 
y 
.
1Primero sustituimos los vértices en la fórmula del área
.
2Aplicamos la regla de Sarrus para calcular el determinante
.
3Así, el área buscada es 
, por lo que se concluye que los puntos estan alineados
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Determinar las ecuaciones parametricas del plano x-2y+z-1=0
Hola, me sirvio mucho, con que informacion podria ponerlos como refernecia en mi proyecto?
Hola que bueno que la pagina te ayudo, podrías poner como pagina de internet «Materíal didactico-Superprof».
– Hallar la ecuación de la recta en su forma simétrica que tiene pendiente igual a 3/2 y que intersecta al eje «y» en (0.2)
Buenas tardes,
Me han ayudado muchísimo vuestros apuntes. Sólo tengo una consulta, ¿cómo tendría que calcular la pendiente de una recta en 3 dimensiones, es decir, en el espacio cartesiano (x, y, z)?
En tres dimensiones no se usa la pendiente pues como se usan tres ejes todo cambia, sino más bien el ángulo que se calcula con el vector director de la recta.
Calcule el angulo que forman las rectas A y B sabiendo que sus vectores directores son A(-3,5) B(2,-5)