Temas
Definición y características de las rectas perpendiculares
Dos rectas son perpendiculares si el ángulo que hay entre ellas es de 
. Observa la siguiente figura:
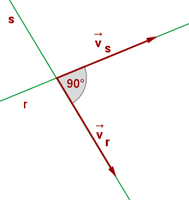
Rectas en el plano
Si las rectas 
y 
se encuentran en el plano euclidiano, entonces estas rectas serán perpendiculares si
1 El producto de las pendientes es 
:
que también se puede ver como
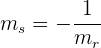
2 o, también si los vectores directores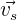 
y 
de las rectas son perpendiculares (es decir, su producto interno es 0):
Nota: las rectas perpendiculares en el plano siempre se cruzan en un único punto. Sin embargo, que las rectas se crucen no es suficiente para decir que las rectas son perpendiculares.
Rectas en el espacio
Cuando las rectas y pertenecen al espacio, entonces la única forma de poder determinar si son perpendiculares es calculando el producto interno de los vectores directores. Este producto debe ser 0:
Nota: en el caso de rectas en el espacio es posible que un par de rectas perpendiculares nunca se crucen.
Nota: dada una recta , entonces existe un número infinito de rectas perpendiculares a esta. Si deseamos encontrar una recta tal que 
, entonces necesitamos más restricciones (por ejemplo, en el plano es suficiente con conocer algún punto por el que pase la recta).
Ejemplos con rectas perpendiculares
1 Encuentra la recta que es perpendicular a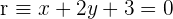 
y que pasa por el punto 
.
Como estamos trabajando con una recta en el plano, entonces podemos encontrar la pendiente de :
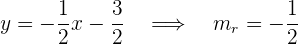
Por tanto, la pendiente de es
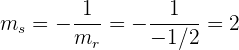
Así, si utilizamos la fórmula punto-pendiente de la recta, obtenemos
Por tanto, la ecuación de la recta perpendicular es
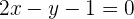
2 Encuentra la ecuación de la recta perpendicular a 
que pasa por el punto 
.
Como la recta se encuentra en el plano, entonces podemos encontrar su pendiente:
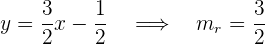
Así, la pendiente de la recta tangente será
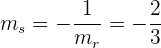
Luego, utilizando la fórmula punto-pendiente para encontrar la ecuación de , con lo que obtenemos
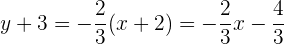
Por tanto, la ecuación de la recta es
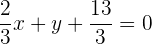
Notemos que podemos multiplica la ecuación por 3 para evitar las fracciones:
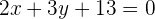
3 Considera las rectas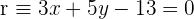 
y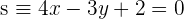 
. Determina la ecuación de la recta que pasa por el punto de interseción de y y que es, además, perpendicular a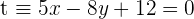 
.
Para poder encontrar la recta 
que es perpendicular a 
, primero debemos encontrar el punto por el que pasa. Esto se hace encontrando la intersección de y , la cual podemos encontrar si resolvermos el siguiente sistema de ecuaciones:
Si despejamos 
de la segunda ecuación, obtenemos
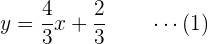
Luego, sustiuimos en la primera ecuación:
por lo tanto, 
. Luego, sustituyendo en (1), obtenemos que 
.
Así, la recta pasa por el punto 
.
Luego, la pendiente de es
por lo que la pendiente de será
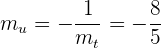
Ahora utilizamos la fórmula punto-pendiente:
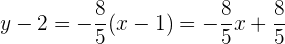
Luego multiplicamos por 5 ambos lados de la ecuación:
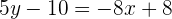
por lo que la ecuación de la recta que es perpendicular a es
4 Encuentra el valor de 
para que las rectas 
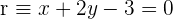y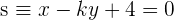 
sean perpendiculares.
Esto lo podemos hacer al notar que el producto de las pendientes de las rectas debe ser . Por tanto, primero encontramos la pendientes de ,
y de ,
Luego, si multiplicamos las pendientes, obtenemos
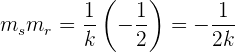
el cual debe ser , es decir,
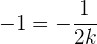
Así, al despejar , obtenemos 
o
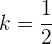
Por lo tanto, debe valer 
para que las rectas sean perpendiculares.
5 Considera las rectas en el espacio dadas por
y
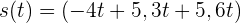
¿Son perpendiculares y ?
Observa que la recta la podemos escribir como
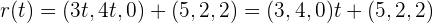
Por tanto, el vector director de es
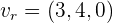
De manera similar, la podemos escribir como
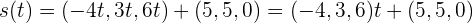
de manera que el vector director de es
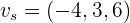
Ahora, el producto interno de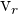 
y 
es
Esto es,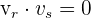 
, por lo tanto 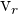y son perpendiculares.
Así, podemos concluir que y sí son perpendiculares.
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
encuentre una forma general de una ecuación de la recta q pasa por el punto A q satisfaga la condicion dada A (5, – 2)
a) paralelo al eje y
b) perpendicular al eje y
¿Cuál es el lugar geométrico descrito por la trayectoria de un avión que se mantiene sobre volando la ciudad de San José a una distancia constante de 5 km de la Torre de Juan Santamaría
Graficar y calcular la distancia y punto Medio de los siguientes P(1,1),Q (3,3)
Hallar la distancia y la pendiente de A(07)
B(2,1)
F(×)=5-2×
A= (7,7)
B= (-9,-6)
Ecuación explícita de la recta
una recta pasa por el punto (0,-5) formando con una x un ángulo de x=90° Hallar la ecuación de la recta
1. Hallar las ecuaciones paramétricas de la recta que pasa por A(3,-1,0) y su vector director sea
perpendicular a los vectores: w = y u =