Temas
Ecuación normal de la recta
Los puntos 
y 
de la recta 
determinan el vector:
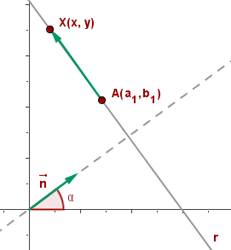
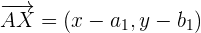
El vector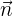 
es un vector unitario y perpendicular a .
Si las componentes del vector director de son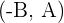 
, las componentes de su vector perpendicular correspondiente son: 
.
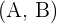Por tanto las componentes del vector unitario y perpendicular serán
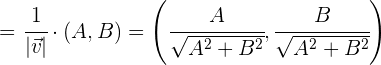
Como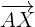 
y 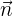son perpendiculares, su producto escalar es cero:
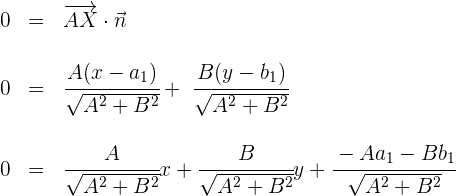
Si en la ecuación general sustituimos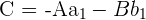 
, obtenemos la ecuación de la recta normal a y que pasa por el punto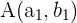 
:
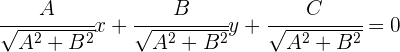
Ejemplo: Hallar la ecuación normal de la recta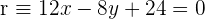 
que pasa por 
.
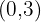Buscamos dos puntos de la recta, para esto le damos valores a 
, por ejemplo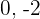 
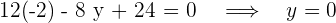
se obtienen dos puntos de la recta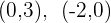 
y con ellos tenemos el vector director de
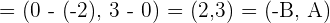
Luego la recta normal buscada es
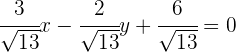
Otra forma de expresar la ecuación normal de la recta es:
Ejemplo: Hallar la ecuación de una recta perpendicular al segmento de extremos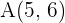 
y 
en su punto medio.
Calculamos el punto medio
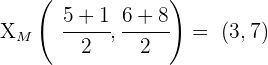
Calculamos el vector director
La recta buscada es
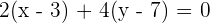
Cosenos directores
Las componentes de un vector unitario en una base ortonormal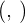 
, son el coseno y el seno que forma con el vector 
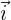de la base.
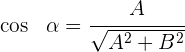
Estas expresiones se llaman cosenos directores de la recta, ya que la segunda puede escribirse como 
.
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
encuentre una forma general de una ecuación de la recta q pasa por el punto A q satisfaga la condicion dada A (5, – 2)
a) paralelo al eje y
b) perpendicular al eje y
¿Cuál es el lugar geométrico descrito por la trayectoria de un avión que se mantiene sobre volando la ciudad de San José a una distancia constante de 5 km de la Torre de Juan Santamaría
Graficar y calcular la distancia y punto Medio de los siguientes P(1,1),Q (3,3)
Hallar la distancia y la pendiente de A(07)
B(2,1)
F(×)=5-2×
A= (7,7)
B= (-9,-6)
Ecuación explícita de la recta
una recta pasa por el punto (0,-5) formando con una x un ángulo de x=90° Hallar la ecuación de la recta
1. Hallar las ecuaciones paramétricas de la recta que pasa por A(3,-1,0) y su vector director sea
perpendicular a los vectores: w = y u =