El concepto de base es uno de los mas importantes en álgebra lineal. Básicamente una base es un subconjunto de elementos de nuestro espacio vectorial con la cual podemos expresar todos los vectores en términos de estos.Primero recordemos que tres vectores  ,
,  y
y 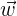 son linealmente independientes en el espacio si uno de ellos no se puede escribir como combinación lineal de los otros dos. Esto implica que los tres vectores tienen distinta dirección.Además los tres vectores
son linealmente independientes en el espacio si uno de ellos no se puede escribir como combinación lineal de los otros dos. Esto implica que los tres vectores tienen distinta dirección.Además los tres vectores  ,
,  y
y 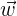 generan todo el espacio si un vector
generan todo el espacio si un vector  cualquiera se puede escribir como combinación lineal de
cualquiera se puede escribir como combinación lineal de  ,
,  y
y 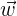 , es decir,
, es decir,
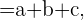
donde  ,
,  y
y  son números reales.
son números reales.
Finalmente, definimos una base del espacio como un conjunto de tres elementos  ,
,  y
y 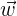 tal que ellos son linealmente independientes y que generan todo el espacio.
tal que ellos son linealmente independientes y que generan todo el espacio.
El ejemplo más destacado de una base de tres vectores es la base canónica, que consiste de los siguientes tres vectores:
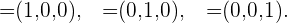
De esta forma las coordenadas de un vector cualquiera  son las siguientes
son las siguientes
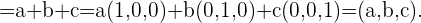

Base ortogonal
Una base de vectores  ,
,  y
y 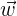 es ortogonal si los vectores de la base son perpendiculares entre sí, es decir,
es ortogonal si los vectores de la base son perpendiculares entre sí, es decir,
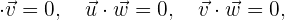
donde  representa el producto interno.
representa el producto interno.
La base canónica es una base ortogonal, ya que sus elemento son perpendiculares entre si.
Base ortonormal
Una base es ortonormal si los vectores de la base son perpendiculares entre sí, y además tienen módulo 1, es decir,

De nuevo podemos decir que la base canónica es ortonormal ya que

Ejemplos de bases ortogonal y ortonormal
1 Dados los vectores 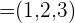 ,
, 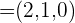 y
y  , demostrar que dichos vectores forman una base y calcula las coordenadas del vector
, demostrar que dichos vectores forman una base y calcula las coordenadas del vector  respecto de dicha base.
respecto de dicha base.
Debemos ver que estos vectores son linealmente, entonces planteamos la siguiente ecuación
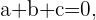

De esto obtenemos el siguiente sistema de ecuaciones,
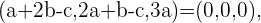

Para saber cuantas soluciones tiene este sistema debemos calcular su determinante, si este es distinto de cero entonces solo tenemos la solución trivial 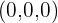 ,
,
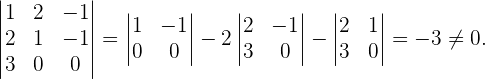
El sistema homogéneo sólo admite la solución trivial:

Por tanto, los tres vectores son linealmente independientes y forman una base.
Ahora buscaremos las coordenadas del vector  con respecto a nuestra base. Para esto planteamos las siguiente ecuación con
con respecto a nuestra base. Para esto planteamos las siguiente ecuación con  ,
,  y
y  número reales,
número reales,
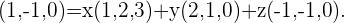
De esto obtenemos el siguiente sistema de ecuaciones del cual obtendremos las solucione para  ,
,  y
y  que representan las coordenadas que buscamos
que representan las coordenadas que buscamos
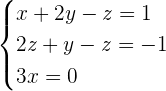
Por inspección obtenemos que  , luego
, luego

lo cual implica que
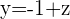
y que

así
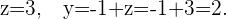
Por lo tanto las coordenadas de  en nuestra base son
en nuestra base son 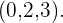
2 Dados los vectores: 
A Demostrar que forman una base.
Los tres vectores forman una base si son linealmente independientes. Para ver esto planteamos la siguiente ecuación y sistema

De esto obtenemos el siguiente sistema de ecuaciones,
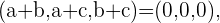
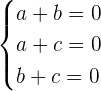
Para saber cuantas soluciones tiene este sistema debemos calcular su determinante, si este es distinto de cero entonces solo tenemos la solución trivial 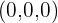 ,
,
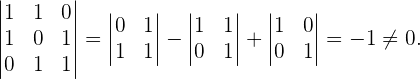
El sistema homogéneo sólo admite la solución trivial:

Por tanto, los tres vectores son linealmente independientes y forman una base.
B Hallar las coordenadas de los vectores de la base canónica respecto de esta base.
Para resolver esto debemos plantear las siguientes tres ecuaciones
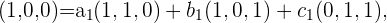
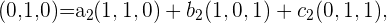

Y hallar los valores para cada 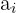 ,
, 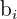 y
y 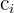 , los cuales son los que determinan las coordenadas para los vectores de la base canónica. Empezamos por la primera ecuación, de la cual obtenemos el siguiente sistema de ecuaciones
, los cuales son los que determinan las coordenadas para los vectores de la base canónica. Empezamos por la primera ecuación, de la cual obtenemos el siguiente sistema de ecuaciones
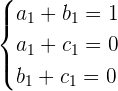
Por inspección tenemos que
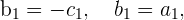
entonces
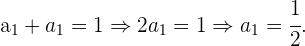
Y por tanto
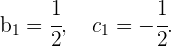
Así que las coordenadas del vector 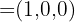 son
son  De la segunda ecuación, obtenemos el siguiente sistema de ecuaciones
De la segunda ecuación, obtenemos el siguiente sistema de ecuaciones
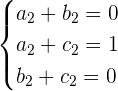
Por inspección tenemos que

entonces

Y por tanto
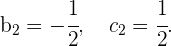
Así que las coordenadas del vector 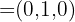 son
son 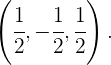 De la ultima ecuación, obtenemos el siguiente sistema de ecuaciones
De la ultima ecuación, obtenemos el siguiente sistema de ecuaciones
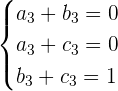
Por inspección tenemos que
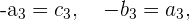
entonces
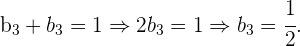
Y por tanto
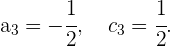
Así que las coordenadas del vector 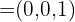 son
son 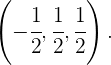
C Calcular el valor de  para que los vectores
para que los vectores 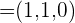 ,
, 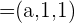 y
y 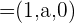 formen una base.
formen una base.
Debemos ver que estos vectores son linealmente independientes. Esto lo comprobamos calculando el determinantes de la matriz formada por ellos. Si el determinante es no nulo entonces ellos son linealmente independientes,
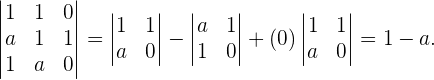
Este determinante es no cero si y solo si 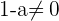 , es decir,
, es decir,  Por lo tanto concluimos que si
Por lo tanto concluimos que si 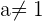 , los vectores forman una base.
, los vectores forman una base.
¿Buscas clases de profe mates? Superprof es tu sitio.













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Sean u = 2i − 3j y v = −4i + 6j. Encuentre: 4v − 6u , con su bosquejo
Al trasladar el punto A(2,4) dado el vector B(2-2) se obtiene?
Hola, de la matriz que calcularon la determinante no es =0.
Podrías señalar el ejercicio para rectificar por favor.
Calcular x²+1
Cómo resolver los ejercicios si están en kilómetros por ejemplo:
A= 300km b=4,000km C= 5,000km
Osea cuando sustituimos tenemos que poner √(X1,X2)² + (Y1,X2)²
O (X2,X1)² +(Y2,Y1)²
¿Cual de las dos?
Depende de que quieras obtener y que significa la expresión (X1,X2), la expresión √(X1,X2)² + (Y1,X2)² esta mal escrita si quieres encontrar una distancia.
24 4 70 NE
Vectores modelo