
Definición de vectores y puntos coplanarios
Dos o más vectores son coplanarios si son linealmente dependientes, y por tanto sus componentes son proporcionales y su rango es 2.
Para que el rango sea igual a 2, el determinante de las componentes de los vectores ha de ser igual a cero.
La forma de calcular un determinante de una matriz de 3x3 es la siguiente:
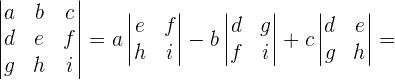
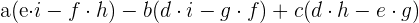
Dos o más puntos son coplanarios, si los vectores determinados por ellos también son coplanarios.
Ejemplos propuestos
1 Comprobar si los puntos 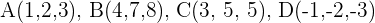 y
y  son coplanarios.
son coplanarios.
Los puntos  y
y 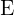 son coplanarios si:
son coplanarios si:
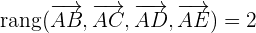


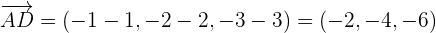
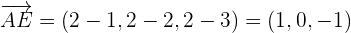



Por lo tanto,
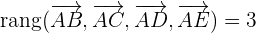
Los puntos A, B, C, D y E no son coplanarios.
2 Determinar el valor de  para que los puntos
para que los puntos  y
y  sean coplanarios.
sean coplanarios.
Para que los puntos sean coplanarios, los vectores determinados por ellos también han de ser coplanarios, es decir, que el rango de los vectores sea 2.
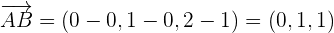

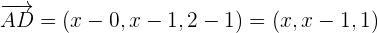
Para que el rango sea igual a 2, el determinante de las componentes de los vectores ha de ser igual a cero.

Por medio determinante encontramos la ecuación a resolver.
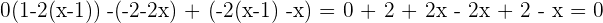
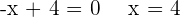
3 ¿Qué en relación se ha de verificar entre los parámetros  y
y  para que los puntos
para que los puntos 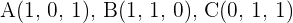 y
y  sean coplanarios?
sean coplanarios?
Los puntos  y
y 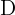 son coplanarios si:
son coplanarios si:

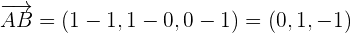


Buscamos que el determinante sea igual a 0
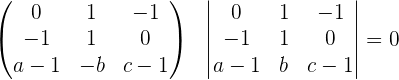
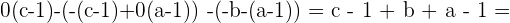
Por lo tanto, la condición para que los puntos sean coplanarios es:

4 Calcular el valor de  para que los puntos
para que los puntos  y
y 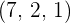 sean coplanarios. Calcular también la ecuación del plano que los contiene.
sean coplanarios. Calcular también la ecuación del plano que los contiene.
Los puntos son coplanares si:

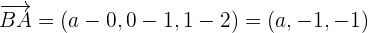
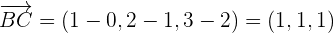
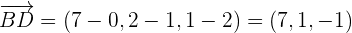
Tenemos que resolver el siguiente siguiente determinante

Ahora vamos a calcular la ecuación del plano


Entonces la ecuación del plano es 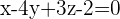













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
encuentre una forma general de una ecuación de la recta q pasa por el punto A q satisfaga la condicion dada A (5, – 2)
a) paralelo al eje y
b) perpendicular al eje y
¿Cuál es el lugar geométrico descrito por la trayectoria de un avión que se mantiene sobre volando la ciudad de San José a una distancia constante de 5 km de la Torre de Juan Santamaría
Graficar y calcular la distancia y punto Medio de los siguientes P(1,1),Q (3,3)
Hallar la distancia y la pendiente de A(07)
B(2,1)
F(×)=5-2×
A= (7,7)
B= (-9,-6)
Ecuación explícita de la recta
una recta pasa por el punto (0,-5) formando con una x un ángulo de x=90° Hallar la ecuación de la recta
1. Hallar las ecuaciones paramétricas de la recta que pasa por A(3,-1,0) y su vector director sea
perpendicular a los vectores: w = y u =